Fibonacci sequence in Javascript

In this post, I present four solutions to compute the $n^{th}$ term of a Fibonacci sequence. The solutions are written in JavaScript (for more fun!).

A Fibonacci sequence is defined as follow: $F(n) = F(n-1) + F(n-2)$ $F_1 = 1$ , $F_2 = 1$

Iterative solutions

This first solution solves the Fibonacci sequence using a for loop. If we count only the arithmetic operations, the solution has a complexity in $o(n)$ ($n-3$ additions in the for loop).

function fibonacci_iter1(n) {
  if (n <= 2) return 1;

  const f = [0, 1, 1];
  for(let i = 3; i <= n; i++) {
    f[i] = f[i-1] + f[i-2];
  }
  return f[f.length-1];
}

While algorithmic complexity is one criterion to evaluate the efficiency of an algorithm, a second criterion is the space complexity, i.e. the amount of memory used by the program. In the previous solution, we stored the $n$ elements of the fibonacci serie in an array, even though technically we would only need to store the rolling last two values. The version below adapts the previous solution by storing only the last two values to decrease the space complexity of the algorithm.

function fibonacci_iter2(n) {
  if (n <= 2) return 1;

  let a = 1, b = 1;
  for(let i = 3; i <= n; i++) {
    let c = a + b;
    a = b;
    b = c;
  }
  return b;
}

Recursive solutions

The version below is a naive recursive solution, if you run it you will see that it takes a lot of time to solve a Fibonacci sequence, even when $n$ is $< 50$.

function fibonacci_recu_naive(n) {
  if (n <= 2) return 1;
  return fibonacci_recu(n-1) + fibonacci_recu(n-2)
}

The reason it takes time is that we compute the same solutions multiple times. As an example, the image below represents the call stack when $n = 5$. We can see that for $n = 1, 2$ and $3$, our naive recursive solution computes the value multiple times.

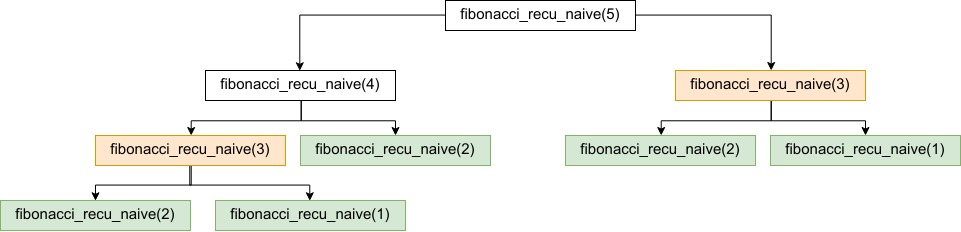
Finally, below we propose another recursive solution that exploits tail recursivity. A tail recursion is a recursive function in which no computation is done after the return of recursive call. Many compilers optimize to change a recursive call to a tail recursive or an iterative call.

function fibonacci_recu_tail(n, a, b) {
  if (n <= 2) return a;
  return fibonacci_recu_tail(n-1, a+b, a);
}

The image below presents the call stack for $n = 5$.



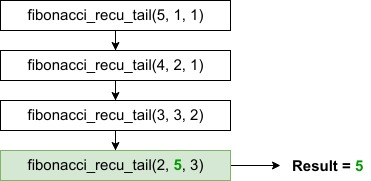
As we can see, the solution is more efficient since we don’t compute the same Fibonacci sequences multiple times as it was the case with the previous solution.