Algorithme du gradient
L’algorithme du gradient est un algorithme d’optimisation. Son objectif est de minimiser une fonction de coût définie par un ensemble de paramètres.
Dans notre exemple nous nous intéresserons à la régression linéaire. Le but est d’approximer un ensemble de points par une droite d’équation y = a*x +b. L’objectif sera d’estimer la valeur des coefficients a et b permettant d’obtenir la droite passant au plus près de l’ensemble des points.
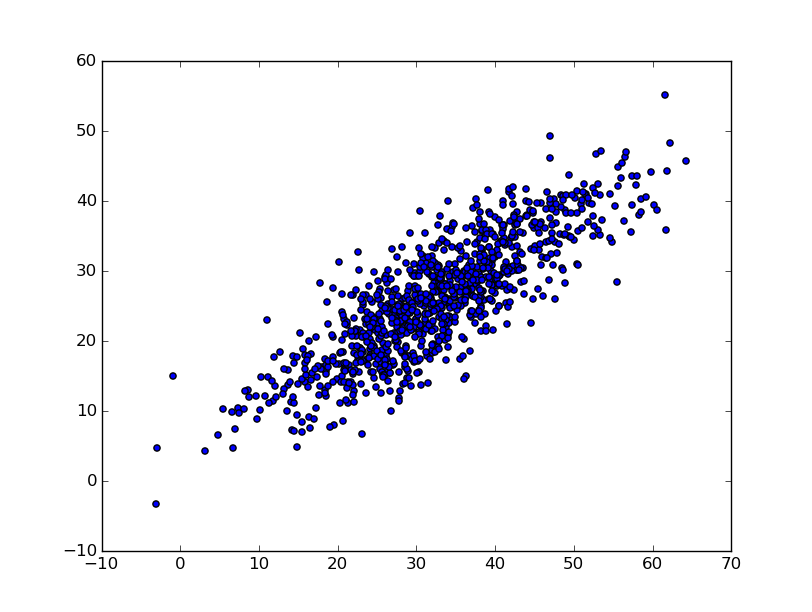
Pour arriver à trouver ces coefficients, il importe de définir un critère de précision. Celui-ci nous permettra de savoir si nos coefficients sont meilleurs ou moins bons. Nous utiliserons l’erreur quadratique moyenne définie de la manière suivante :
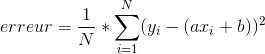
Pour appliquer l’algorithme du gradient sur cette fonction d’erreur, nous devons commencer par calculer son gradient. Comme notre fonction dépend de deux paramètres, nous devons calculer les dérivées partielles par rapport à chacun de nos paramètres (a et b) :
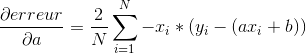
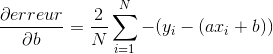
Nous pouvons désormais appliquer notre algorithme. Tout d’abord nous allons commencer par générer des couples de données (x,y) linéairement corrélés :
import numpy as np
#premiere etape : generer des donnees x, y correlees lineairement
def genererDonnees():
xx = np.array([0.8, 65])
yy = np.array([0.45, 51.5])
means = [xx.mean(), yy.mean()]
stds = [xx.std() / 3, yy.std() / 3]
corr = 0.85
covs = [[stds[0]**2, stds[0]*stds[1]*corr],
[stds[0]*stds[1]*corr, stds[1]**2]]
points = np.random.multivariate_normal(means, covs, 1000).T
return pointsNous devons choisir une valeur initiale pour nos coefficients a et b. Ici, nous choisirons 0. Lors de chaque itération nous mettrons à jour la valeur de a et b de manière à faire décroître l’erreur quadratique. La direction pour faire varier a et b est déterminée grâce aux dérivées partielles que nous avons déterminées précédemment :
def iterationGradient(points, a, b, tauxApprentissage):
gradientA = 0
gradientB = 0
N = float(len(points[0]))
for i in range(0, len(points[0])):
gradientB += -(2/N) * (points[1][i] - (a*points[0][i]) + b)
gradientA += -(2/N) * points[0][i] * (points[1][i] - (a * points[0][i]) + b)
#on met a jour a et b
b = b - (tauxApprentissage * gradientB)
a = a - (tauxApprentissage * gradientA)
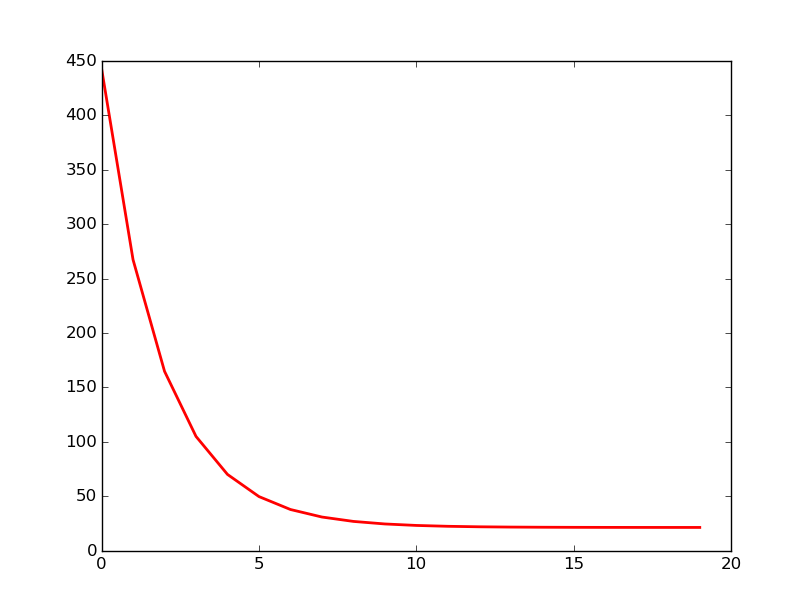
return a,bLa variable tauxApprentissage indique si lors de chaque itération on décide de faire varier beaucoup ou peu les valeurs de a et b. Comme nous pouvons le voir sur le graphique ci-dessous qui représente l’erreur quadratique moyenne en fonction du nombre d’itérations effectuées, l’erreur décroit rapidement pour se stabiliser aux alentours de 25 au bout d’une dizaine d’itérations :
Voici le reste du code qui permet l’initialisation des variables ainsi que l’appel de la fonction iterationGradient :
def gradientDescent(points, aInitial, bInitial, tauxApprentissage, nbIterations):
a = aInitial
b = bInitial
for i in range(nbIterations):
a, b = iterationGradient(points, a, b, tauxApprentissage)
return a,b
def estimationsParametres():
tauxApprentissage = 0.0001
aInitial = 0
bInitial = 0
nbIterations = 20
donnees = genererDonnees()
a,b= gradientDescent(donnees, aInitial, bInitial, tauxApprentissage, nbIterations)
return a,b
a, b = estimationsParametres()
#a = 0.776207203202
#b = 0.02282254121Graphiquement nous obtenons la droite suivante qui passe relativement près de l’ensemble des points :
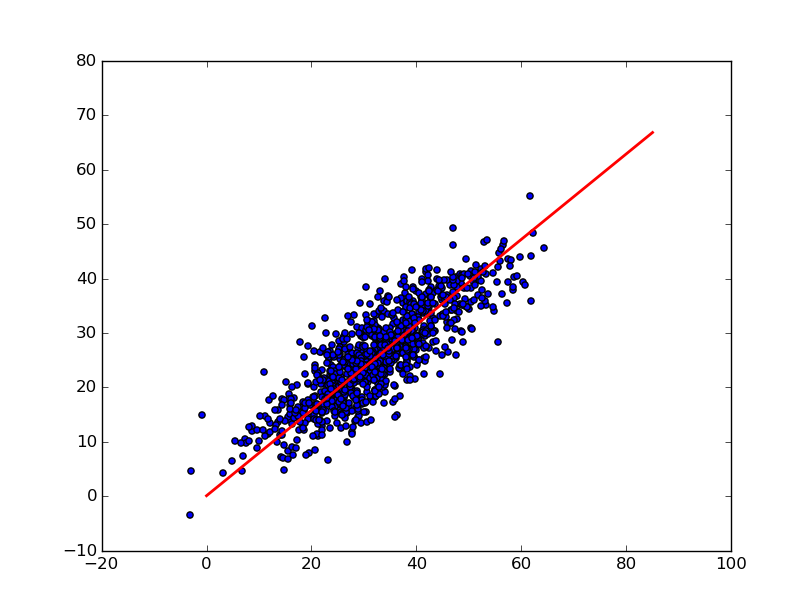
Dans notre exemple nous définissons un nombre d’itérations fixe. Une solution plus appropriée serait de définir un critère comme la diminution de l’erreur entre deux itérations.
